Contact

What is Fluid Dynamics?

In the context of micro dispensing, fluid dynamics focuses on the precise control of tiny volumes of liquids as they move through nozzles, channels, or valves. It examines how fluid properties like viscosity, surface tension, and flow rate affect droplet formation and placement. Accurate fluid dynamics is critical to ensure consistent, repeatable dispensing without clogging or splashing.
Key Elements

Why is it important?

Fluid dynamics is the study of fluids in motion. Getting the right conditions for accurate and repeatable aliquot dispensing or pumping in microvolume applications at the Industrial scale requires more than a little luck. It involves determining the key elements that govern the fluid’s behaviour. Understanding and more importantly controlling how the fluid travels throughout the fluid path is critical to ensure consistent delivery in micro volume dispensing and metering applications.

Optimisation is Key!

The fluid path includes everything from the vessel that contains the liquid all the way to the point of dispense. It is only the beginning once the preliminary specifications of the fluid path have been determined. Through our understanding of fluid dynamics and our experience in micro volume dispensing we optimise components and tuning of the control system to maximise your system performance.

If you want to optimise your manufacturing process to Increase Yield while Reducing Defects, Downtime, Costs and Waste, contact us

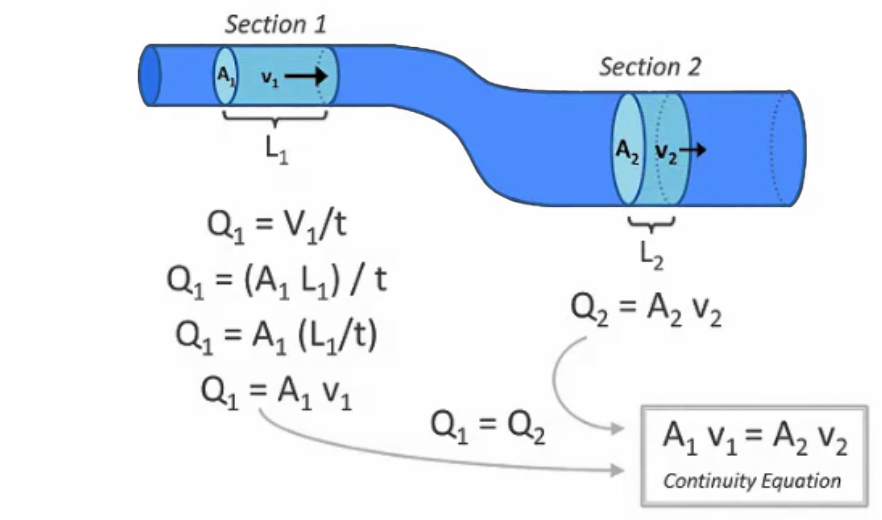
Many factors influence Fluid Dynamics. Here follows a brief explanation of some of the key elements and principles that govern fluid behaviour we consider when designing and building microvolume dispensing systems.

1. Continuity Equation

Based on the principle of mass conservation, it ensures that the mass of fluid entering a system equals the mass leaving it.
Section 1 and Section 2 are the same volume. What goes in must come out!

.

2. Momentum Equation (Navier-Stokes Equations)

Describes how forces (pressure, viscosity, and external forces) affect fluid motion.

Based on Newton’s Second Law: F = ma

General Form:

.

3. Energy Equation

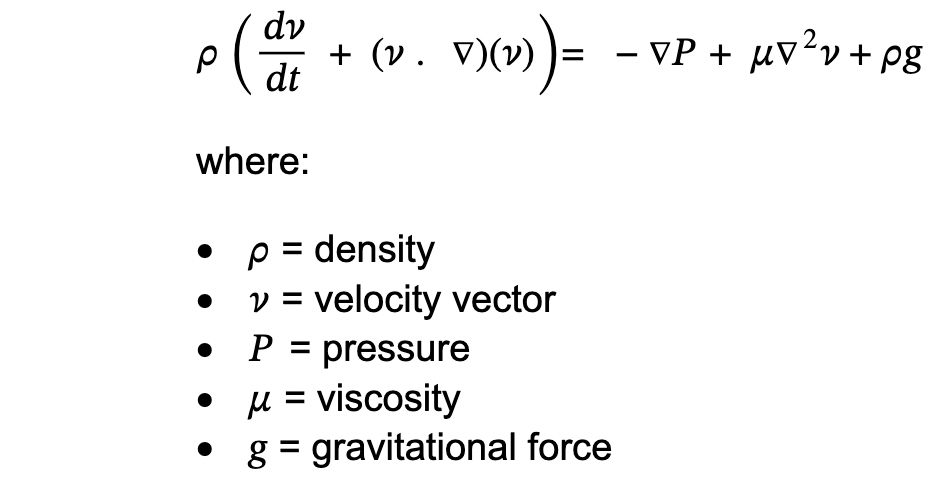
The energy equation in fluid dynamics is a mathematical representation of the conservation of energy principle, specifically applied to fluid flow. It accounts for how energy is transferred within a fluid system due to work done, heat transfer, and internal energy changes.

General Form of the Energy Equation

In its most general form, the energy equation is written as:
This equation essentially states that the total energy of a fluid particle (kinetic, potential, and internal energy) changes due to heat transfer, work done by viscous forces, and energy dissipation due to heat conduction.

.

4. Bernoulli’s Equation

Is a simplified version of the energy equation for incompressible, non-viscous, steady flow.

.

5. Viscosity

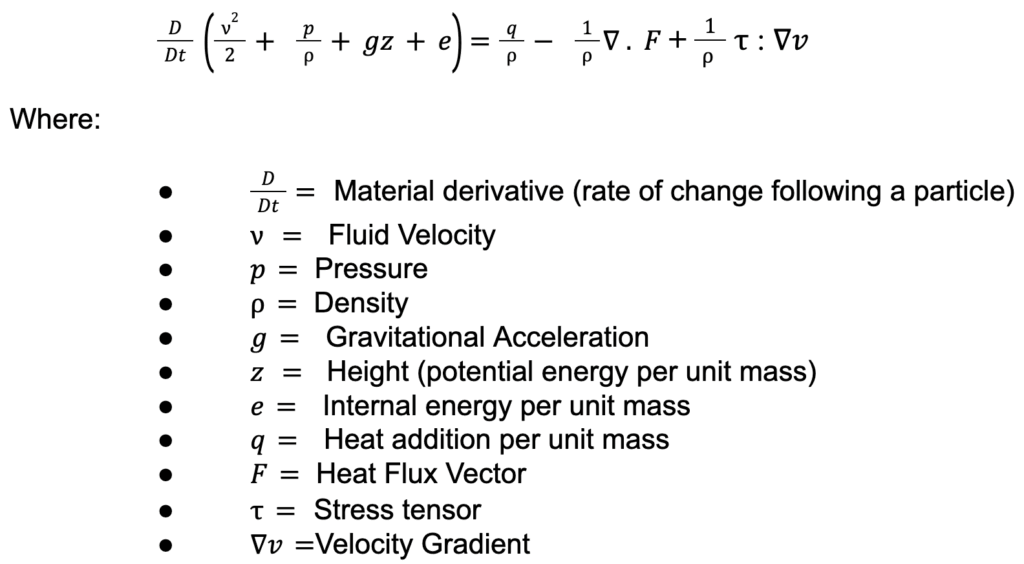
Viscosity (𝜇) is a measure of a fluid’s resistance to deformation or flow due to internal friction between its layers. It plays a crucial role in fluid dynamics, particularly in the Navier-Stokes equations (Momentum Equations) and the analysis of laminar and turbulent flow.

The relationship between viscosity and shear rate (also called the shear rate or flow rate) is central to understanding the flow behaviour of fluids.

Here’s how they interact:

  • Viscosity is a measure of a fluid’s resistance to flow. It quantifies the internal friction within the fluid as molecules move past one another. The higher the viscosity, the thicker or more resistant the fluid is to flowing.
  • Shear rate refers to the rate at which adjacent layers of fluid move relative to each other. It is typically measured in units of reciprocal seconds (s⁻¹).

The relationship between viscosity and shear rate can vary depending on the type of fluid:

5a Newtonian Fluids (such as water, honey and air) follow Newton’s Law of Viscosity which details the linear relationship between shear stress (𝜏) and velocity gradient (𝑑𝑢/𝑑𝑦), represented by the formula:

This equation states that shear stress is directly proportional to the rate of strain, with viscosity a(μ) acting as the proportionality constant.

Newtonian fluids (like Water, Honey, Silicone Oils or Air), behave predictably, and changes in shear rate do not alter the viscosity.

Unfortunately, the majority of fluids do not exhibit Newtonian behaviour and an understanding of their Rheology is required to predict and control their flow behaviour.

5.b Non-Newtonian Fluids

Viscosity appears explicitly in the Navier-Stokes equations, which aNon-Newtonian fluids, like ketchup or blood, exhibit a variable viscosity depending on the shear rate. This means that the viscosity can change as the fluid is subjected to different shear rates.

There are several types of Non-Newtonian behaviour:

  • Shear-thinning (Pseudoplastic): In these fluids, viscosity decreases as shear rate increases (e.g., paint or blood).
  • Shear-thickening (Dilatant): In these fluids, viscosity increases as shear rate increases (e.g., cornstarch in water).
  • Dilatant Behaviour – Walking on Custard, under low shear the custard behaves like a liquid but exhibits solid behaviour under high shear.
  • Bingham Plastics: These fluids have a yield stress, meaning they act like a solid until a certain shear stress threshold is exceeded. Once the yield stress is overcome, they flow like a fluid with constant viscosity.

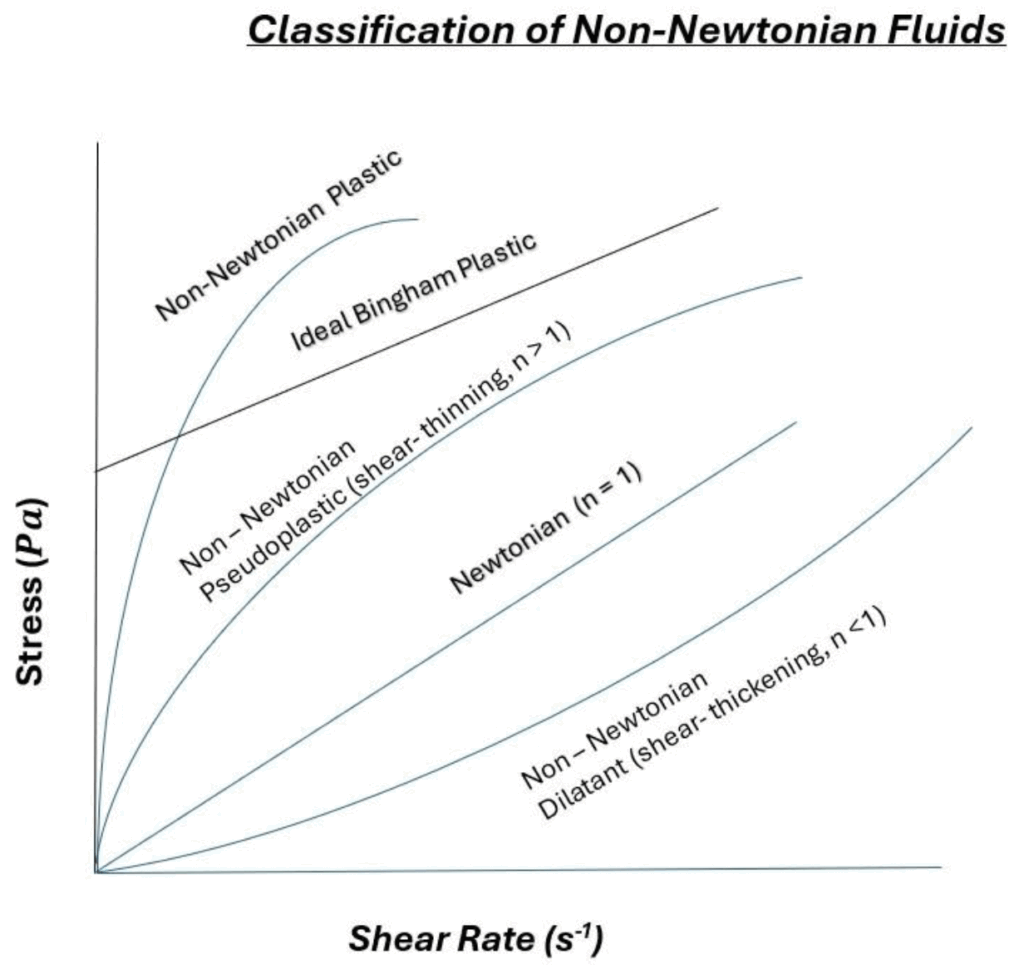
Other Non-Newtonian behaviours are Time Dependent.

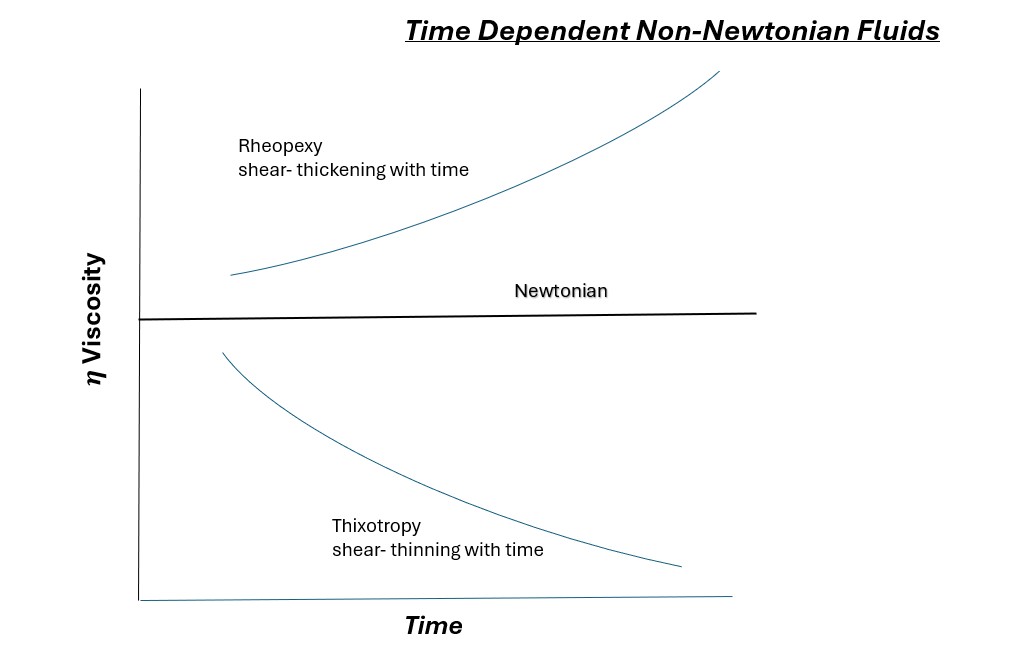
Under conditions of constant shear rate some fluids will display a change in viscosity with time.

There are two categories to consider:

  • THIXOTROPY: A thixotropic fluid undergoes a decrease in viscosity with time, while it is subjected to a constant shear rate.
  • RHEOPEXY: Essentially the opposite of thixotropic behaviour, in that the fluid’s viscosity increases with time as it is sheared at a constant rate.

Both thixotropy and rheopexy may occur in combination with any of the previously discussed flow behaviours, or only at certain shear rates.

The time element is extremely variable; under conditions of constant shear, some fluids will reach their final viscosity value in a few seconds, while others may take up to several days.

Rheopectic fluids are rarely encountered. Thixotropy, however, is frequently observed in materials such as greases, heavy printing inks, and paints.

Because of the range of behaviours multiple models are required to Characterise Non-Newtonian Fluid behaviour.

The Power Law  fluid model is the simplest and perhaps most commonly employed model. It gives a basic relation for viscosity,  𝜈, and the shear rate,  𝛾. In this model, the value of viscosity can be bounded by a lower bound value,  𝜈 min, and an upper bound value,  𝜈 max.

The relation is given as: 𝜈 = 𝜅 . 𝛾𝜂−1 Where:
  • 𝜅  is the flow consistency index [m2/s],
  • 𝛾  is the shear rate [s−1],
  • 𝜂  is the flow behaviour index.
Based on the flow behaviour index, η:
  • if 0< 𝜂 <1: The fluid shows pseudo-plastic or shear-thinning behaviour. Here a smaller value of n means a greater degree of shear-thinning.
  • if  𝜂 =1: The fluid shows Newtonian behaviour.
  • if  𝜂 >1: The fluid shows dilatant or shear-thickening behaviour with a higher value of n resulting in greater thickening.

A limitation of the Power Law Model is that it is only valid over a limited range of Shear rates. As required this can be addressed by utilising Bird-Carreau and Cross-Power Law  models to cover the entire Shear Rate Range. The Herschel–Bulkley  model is also used to evaluate non-Newtonian fluids. This model combines the behaviour of Bingham and power-law fluids in a single relation.

5.c Kinematic Viscosity (ν)
Another important form of viscosity is kinematic viscosity (𝜐), which is defined as:
Kinematic viscosity is useful in non-force-based flow analysis, such as in Reynolds number calculations which are important in Turbulence Classification.

Summary: 

  • Newtonian fluids: Viscosity is constant regardless of shear rate. 
  • Non-Newtonian fluids – Shear Dependency: Viscosity changes with shear rate. For shear-thinning fluids, viscosity decreases as shear rate increases, and for shear-thickening fluids, viscosity increases as shear rate increases. 
  • Non-Newtonian fluids – Time Dependency: Viscosity changes over time at constant shear rate. Thixotropic decrease over Time, Rheopectic increase over Time. Time element can be seconds or days depending on the material. 

.

6. Reynolds Number

The Reynolds number (Re) is a dimensionless quantity (no unit of measure) in fluid dynamics that predicts whether fluid flow is laminar or turbulent. It represents the ratio of inertial forces to viscous forces within a fluid. A low Reynolds number indicates laminar flow (smooth, predictable), while a high Reynolds number suggests turbulent flow (chaotic, unpredictable).

  • In Laminar Flow fluid particles move in parallel layers with minimal mixing. This occurs at low Reynolds numbers, where viscous forces dominate and prevent the chaotic movement of turbulent flow.
  • In Turbulent Flow fluid particles move chaotically, creating eddies and swirls. This occurs at high Reynolds numbers, where inertial forces dominate and disrupt the smooth flow of the fluid.
If turbulence occurs (e.g., due to high-speed actuation or improper nozzle geometry), it can introduce variability in drop formation, jet breakup, and dosing accuracy. We design and tune the fluid to keep the flow laminar, so that fluid behaviour is stable and repeatable. Turbulence may be a sign of poor design or inappropriate operating conditions.

.

7. Turbulence & Boundary Layers

  • Turbulent Flow: Chaotic, irregular motion with eddies and vortices.
  • Boundary Layer: The thin layer of fluid near a surface where velocity changes from zero (at the surface) to the free stream velocity.

In designing or optimizing a micro dispensing system, our focus is on controlling boundary layer effects and avoiding turbulence to ensure high accuracy, repeatability, and consistency.

Contact Us

Get in touch with us below to get started. Feel free to call us on +353 (0)46 900 9050 or email
info@industrial-fluidics.com

Get in touch with us below to get started. Feel free to call us on
+353 (0)46 900 9050 or email
info@industrial-fluidics.com

"*" indicates required fields

This field is for validation purposes and should be left unchanged.

Contact Us

T: +353 (0)46 900 9050

E: info@industrial-fluidics.com

Monday – Friday: 9am-5pm

About

Our Services

Useful Links

2025 Industrial Fluidics Terms of Service Privacy Policy Cookie Policy Website by Effector